 2х² - 6х + 5 < 0. 7-х=2. 5х2-20=0. х4+4х3-2х2-4х-3=0. полное и неполное приведенное и неприведенное уравнение. 2х² - 6х + 5 < 0. 7-х=2. 5х2-20=0. х4+4х3-2х2-4х-3=0. полное и неполное приведенное и неприведенное уравнение. |  х 3 х 2 9х 18. х4 + 4х3 – 2х2 – 12х + 9 = 0. х 3 х 2 9х 18. решение уравнения 9^2х- 9 ^х-6=0. х2-9. х 3 х 2 9х 18. х4 + 4х3 – 2х2 – 12х + 9 = 0. х 3 х 2 9х 18. решение уравнения 9^2х- 9 ^х-6=0. х2-9. |
 решение уравнения 2х 18-х. 3х-6=х. х 3 х 2 9х 18. х2-х-2=0. 4х-3/2-5-2х/3-3х-7/6=0. решение уравнения 2х 18-х. 3х-6=х. х 3 х 2 9х 18. х2-х-2=0. 4х-3/2-5-2х/3-3х-7/6=0. |  (х-9)(2-х)=0. х 3 х 2 9х 18. х 3 х 2 9х 18. -х-2=9х. 6х-2<2х+6. (х-9)(2-х)=0. х 3 х 2 9х 18. х 3 х 2 9х 18. -х-2=9х. 6х-2<2х+6. |
 2\3х +5\6х-7\9х=1\2. 5х2–2х-1=0. х3 2х2 9х 18 х-3 х+2. х8 · х3. х 3 х 2 9х 18. 2\3х +5\6х-7\9х=1\2. 5х2–2х-1=0. х3 2х2 9х 18 х-3 х+2. х8 · х3. х 3 х 2 9х 18. | 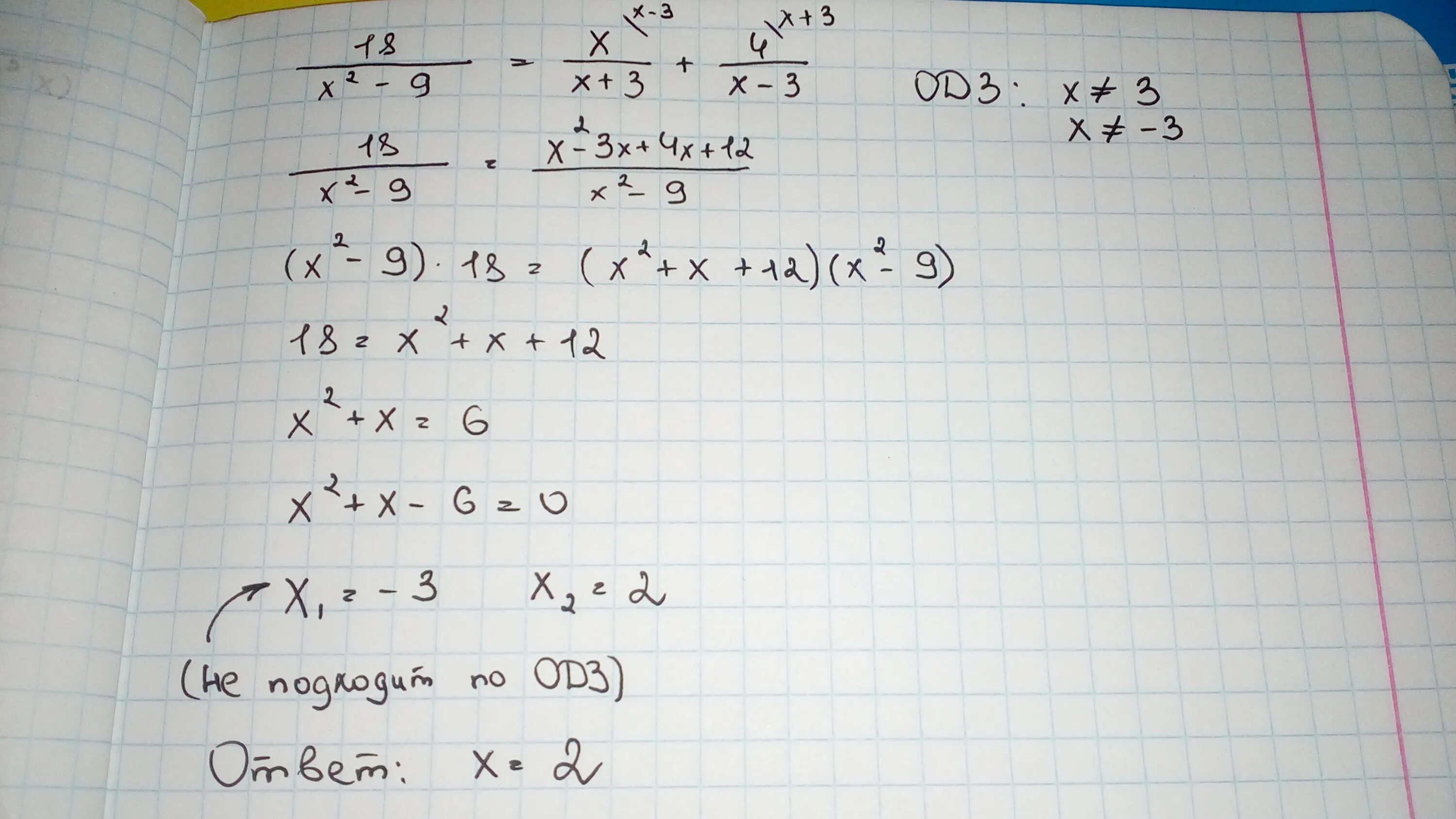 х 3 х 2 9х 18. 3/х+3+3/х2-3х+2х/9-х2. х3+2х2-9х-18 0. -7( 2-2+3х)-2х=-9. (x^2-2x+2)^2. х 3 х 2 9х 18. 3/х+3+3/х2-3х+2х/9-х2. х3+2х2-9х-18 0. -7( 2-2+3х)-2х=-9. (x^2-2x+2)^2. |
 х 3 х 2 9х 18. решите уравнение 2х-3(х+3)=-5. -3х-9=2х. -5х+6=0. х3+5х2-4х-20 0. х 3 х 2 9х 18. решите уравнение 2х-3(х+3)=-5. -3х-9=2х. -5х+6=0. х3+5х2-4х-20 0. |  х^2-4х+3=0 решение уравнения. 5х4+9х3-2х2-4х-8. 2х-(7+х)=2. полное неполное приведенное неприведенное. решение уравнения 9х=9х. х^2-4х+3=0 решение уравнения. 5х4+9х3-2х2-4х-8. 2х-(7+х)=2. полное неполное приведенное неприведенное. решение уравнения 9х=9х. |
 х3+6х2 9х+54. 2х+7х-9=0. 9х²-7х-2=0. 2х(8х-3)-5х(3х+2). х2-9: х3-3х2+4х-12. х3+6х2 9х+54. 2х+7х-9=0. 9х²-7х-2=0. 2х(8х-3)-5х(3х+2). х2-9: х3-3х2+4х-12. |  х 3 х 2 9х 18. 6х2-3х=0. х 3 х 2 9х 18. решение уравнений 2(х-9)=9. х^2/х^2-9=12-7х/9-х^2. х 3 х 2 9х 18. 6х2-3х=0. х 3 х 2 9х 18. решение уравнений 2(х-9)=9. х^2/х^2-9=12-7х/9-х^2. |
 х2+2х2-9х-18/(х-3)(х+2). х4-4х3-7х2+12х+24 / х3-3х2 +2. 3х2 18х решение. х 3 х 2 9х 18. х 3 х 2 9х 18. х2+2х2-9х-18/(х-3)(х+2). х4-4х3-7х2+12х+24 / х3-3х2 +2. 3х2 18х решение. х 3 х 2 9х 18. х 3 х 2 9х 18. |  приведенные и неприведенные квадратные уравнения. х4=(х-20)2. (х в 2 +2х) в 2 + (х+1) в 2=57. х 3 х 2 9х 18. 2/х+4-3/х-4=0 , х2+20/х2-4=х-3/х+2-6/2-х. приведенные и неприведенные квадратные уравнения. х4=(х-20)2. (х в 2 +2х) в 2 + (х+1) в 2=57. х 3 х 2 9х 18. 2/х+4-3/х-4=0 , х2+20/х2-4=х-3/х+2-6/2-х. |
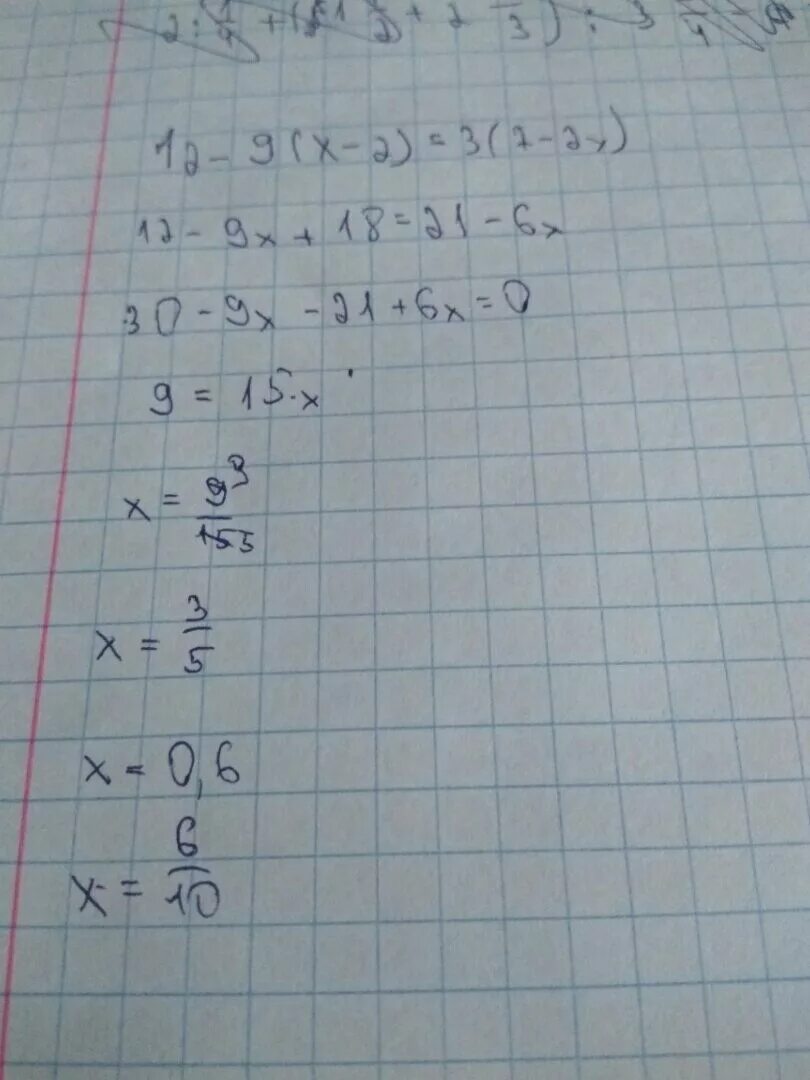 -2(х+3)+4(х-1). х3 2х2 9х 18 х-3 х+2. х 3 х 2 9х 18. х2-9/х3+2х2+9. сократите дробь х3+2х2-9х-18 х-3 х+2. -2(х+3)+4(х-1). х3 2х2 9х 18 х-3 х+2. х 3 х 2 9х 18. х2-9/х3+2х2+9. сократите дробь х3+2х2-9х-18 х-3 х+2. | 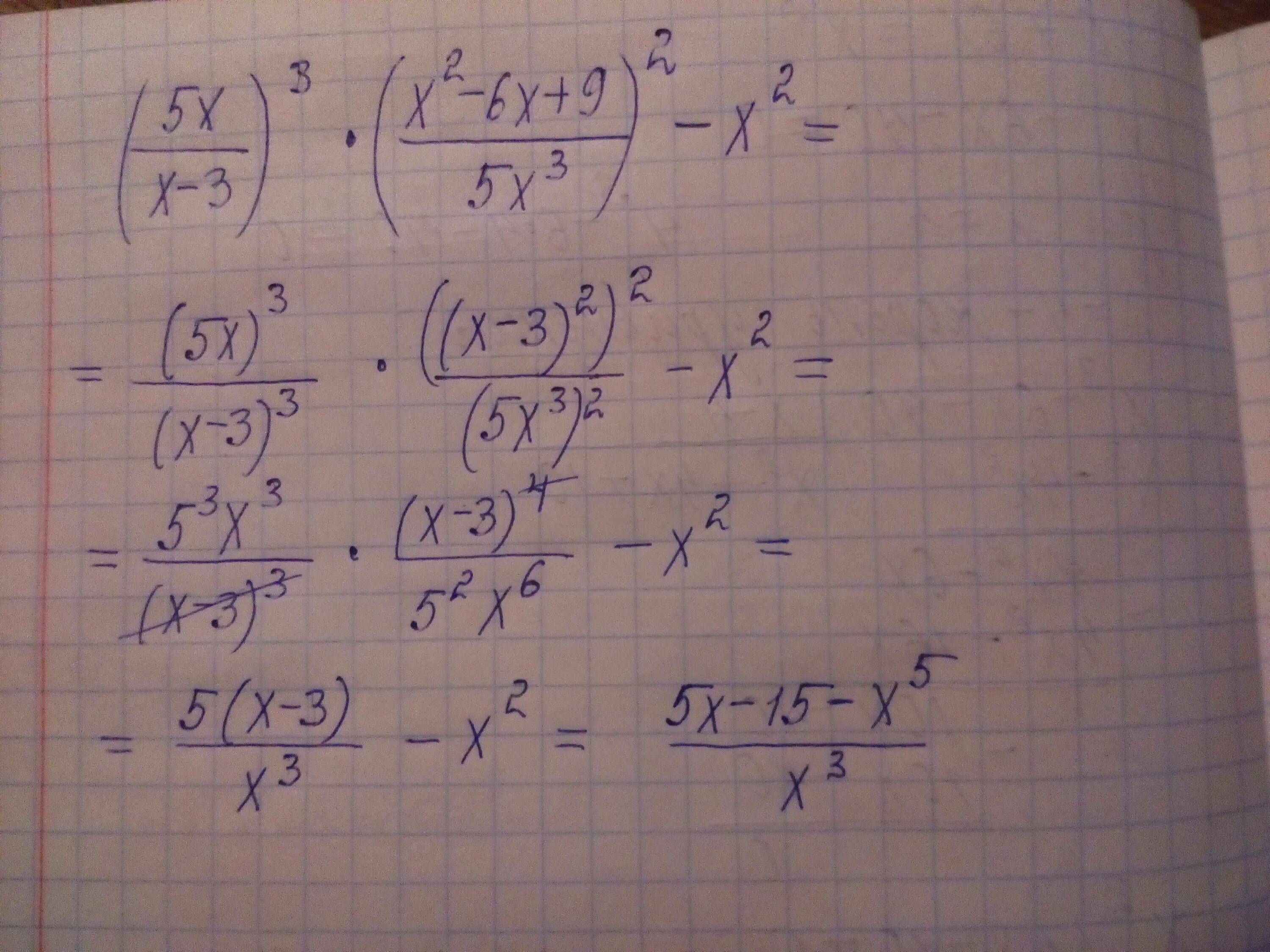 х^2/х+3=9/х+3. 2х+1/3-4х-х2/12 х2-4/9. х(2-х)/3+3(х-2)/2=2 |1/4-2(4-х)/6^2. х 3 х 2 9х 18. неполное квадратное уравнение 3x^2-5x. х^2/х+3=9/х+3. 2х+1/3-4х-х2/12 х2-4/9. х(2-х)/3+3(х-2)/2=2 |1/4-2(4-х)/6^2. х 3 х 2 9х 18. неполное квадратное уравнение 3x^2-5x. |
 х 3 х 2 9х 18. сократите дробь х2+2х-9х-18/(х-3). X3 - 2x3 + 3x4 0 3x1 + 8. х2-9/3х2+х3. X3 + 24x3 - 19. х 3 х 2 9х 18. сократите дробь х2+2х-9х-18/(х-3). X3 - 2x3 + 3x4 0 3x1 + 8. х2-9/3х2+х3. X3 + 24x3 - 19. |  уравнение 3х+2 =-х. х 3 х 2 9х 18. (х+3)(х-2)(3х-9)<0. х 3 х 2 9х 18. (х2-3х+2)/(9-х2)≥0. уравнение 3х+2 =-х. х 3 х 2 9х 18. (х+3)(х-2)(3х-9)<0. х 3 х 2 9х 18. (х2-3х+2)/(9-х2)≥0. |
 (х-2)"2/2 + 18/(х-2)"2 = 7(х-2/2-3/х-2). х 3 х 2 9х 18. -х-2=9х. X4 - 0. {х1−4х2- 3х3=8,3х1− 2х2 3х3= 2,5х1- х2 2х3= 33. (х-2)"2/2 + 18/(х-2)"2 = 7(х-2/2-3/х-2). х 3 х 2 9х 18. -х-2=9х. X4 - 0. {х1−4х2- 3х3=8,3х1− 2х2 3х3= 2,5х1- х2 2х3= 33. |  х 3 х 2 9х 18. ( x1 + 2x2 + 4x3 - 3x4 = 0 3x1 - 5x2 6x3 - 4x4 - 0 4x1 + 5. х^4+x^3. 5х-3>1+х 1/2-3х<2/3х-5. х2 +9х +18=0 х2-4х-21=0. х 3 х 2 9х 18. ( x1 + 2x2 + 4x3 - 3x4 = 0 3x1 - 5x2 6x3 - 4x4 - 0 4x1 + 5. х^4+x^3. 5х-3>1+х 1/2-3х<2/3х-5. х2 +9х +18=0 х2-4х-21=0. |
 х-9/х2-9-3/3х-х2. х3 2х2 9х 18 х-3 х+2. (4 х - 5) 2 + 2*4х = 9 модуль4х -5. 1/5х+4=2 1/3. 3х-х+2/4-3х-2/2+х-1/3=1. х-9/х2-9-3/3х-х2. х3 2х2 9х 18 х-3 х+2. (4 х - 5) 2 + 2*4х = 9 модуль4х -5. 1/5х+4=2 1/3. 3х-х+2/4-3х-2/2+х-1/3=1. |  3-х/3=х/2. 5х-2>8. х3 2х2 9х 18 х-3 х+2. х+2(х+9)=3х+18. 3-х/3=х/2. 5х-2>8. х3 2х2 9х 18 х-3 х+2. х+2(х+9)=3х+18. |



































