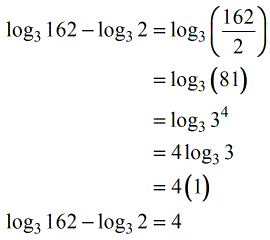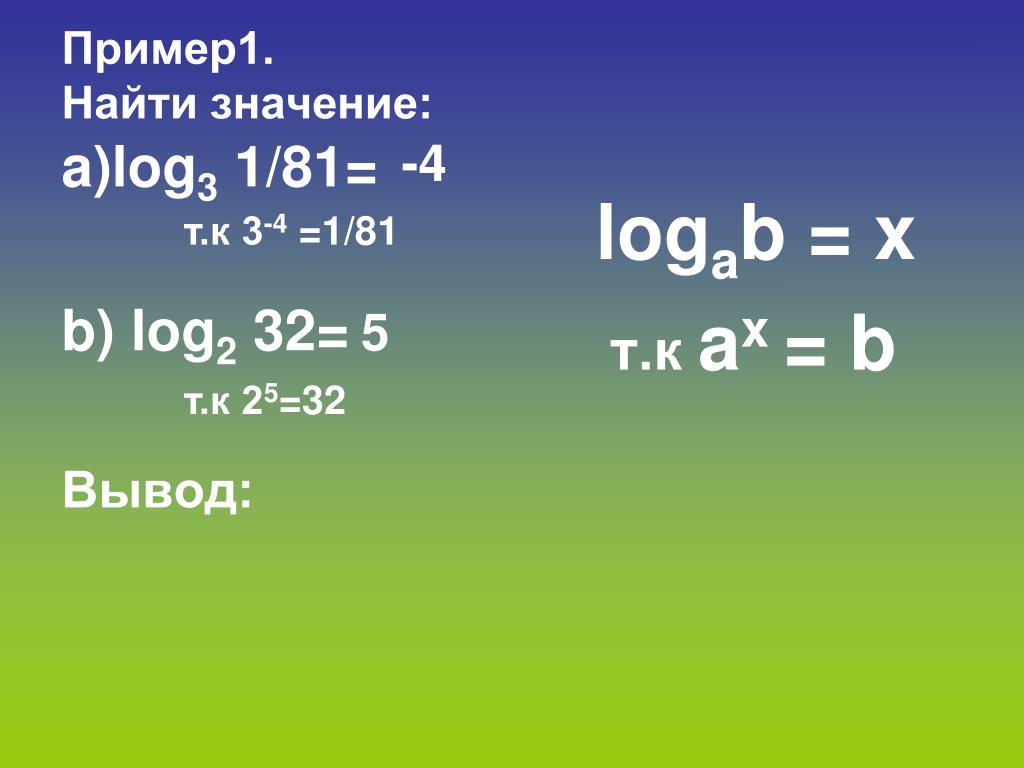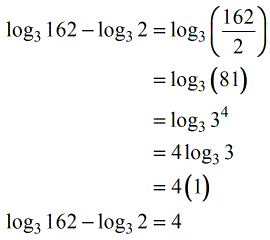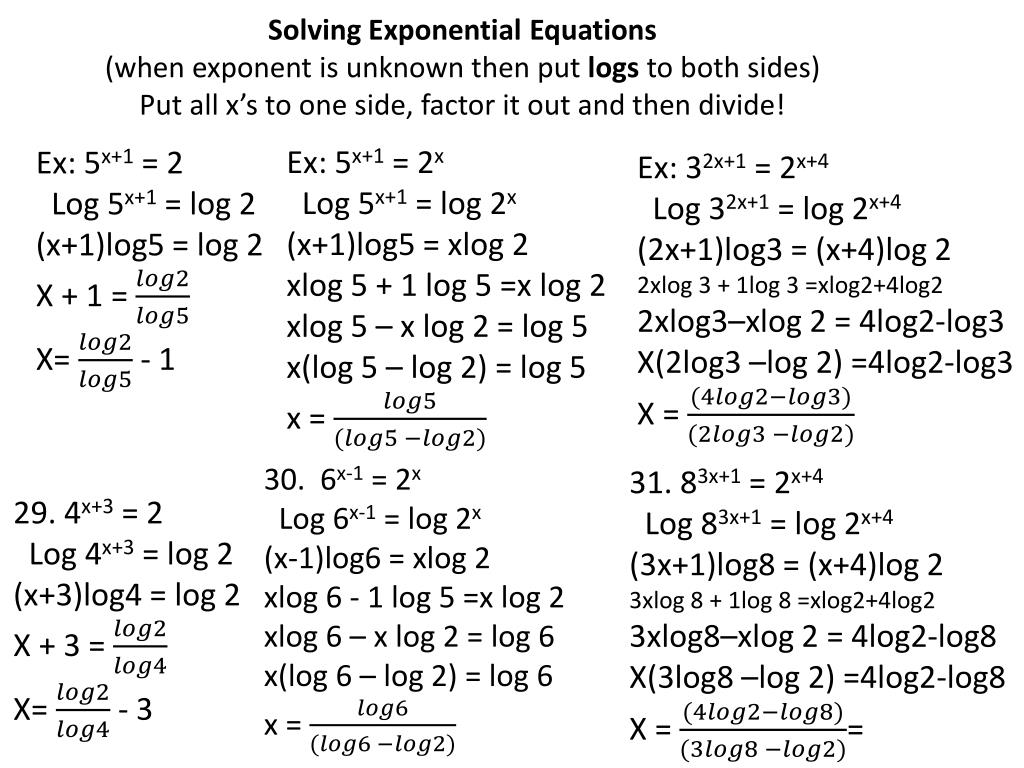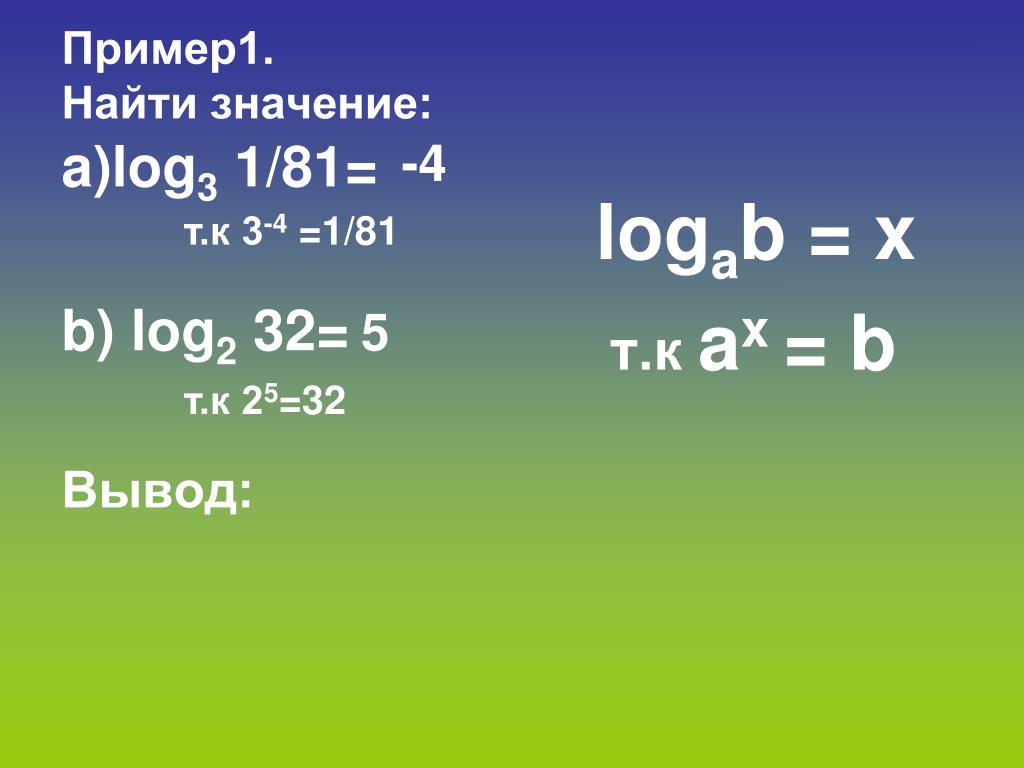Log2 2 𝑥 − 2 log2 𝑥 − 3 = 0. 3 1 log3 4. Log16 x 5 log x 2+10x+25 2 3 4. Log 1. Log4x=2.
Log2 2 𝑥 − 2 log2 𝑥 − 3 = 0. 3 1 log3 4. Log16 x 5 log x 2+10x+25 2 3 4. Log 1. Log4x=2.
|
 3 1 log3 4. Log4x>1. 3 1 log3 4. Log2 log2 4 корень. Log2 4+log2 корень из 10.
3 1 log3 4. Log4x>1. 3 1 log3 4. Log2 log2 4 корень. Log2 4+log2 корень из 10.
|
 Лог 3 3. 3 1 log3 4. Log 81 по основанию 3. 2^log4(x+1)=3. Lg0.
Лог 3 3. 3 1 log3 4. Log 81 по основанию 3. 2^log4(x+1)=3. Lg0.
|
 5. Log2 3. \log _(\sqrt(5))4*\log _(49)5*\log _(8)7. Log3 162-log3 2. Log(4x+5)=log1/3( x²+8 x) ответ.
5. Log2 3. \log _(\sqrt(5))4*\log _(49)5*\log _(8)7. Log3 162-log3 2. Log(4x+5)=log1/3( x²+8 x) ответ.
|
 3 1 log3 4. Log2 4 x 2 log2 5. 3 1 log3 4. Log1/2((x-3)(9-x))=-3. Логарифмические уравнения log2/3 + log7.
3 1 log3 4. Log2 4 x 2 log2 5. 3 1 log3 4. Log1/2((x-3)(9-x))=-3. Логарифмические уравнения log2/3 + log7.
|
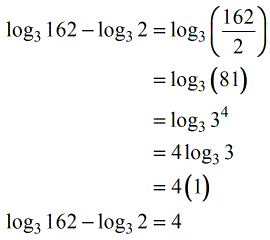 Логарифмические уравнения и неравенства. Log2(log3 9+2). Решения логарифмических уравнений log2 x=1. Решение логарифмических уравнений log3 х. Логарифмические уравнения log1/2 + log3.
Логарифмические уравнения и неравенства. Log2(log3 9+2). Решения логарифмических уравнений log2 x=1. Решение логарифмических уравнений log3 х. Логарифмические уравнения log1/2 + log3.
|
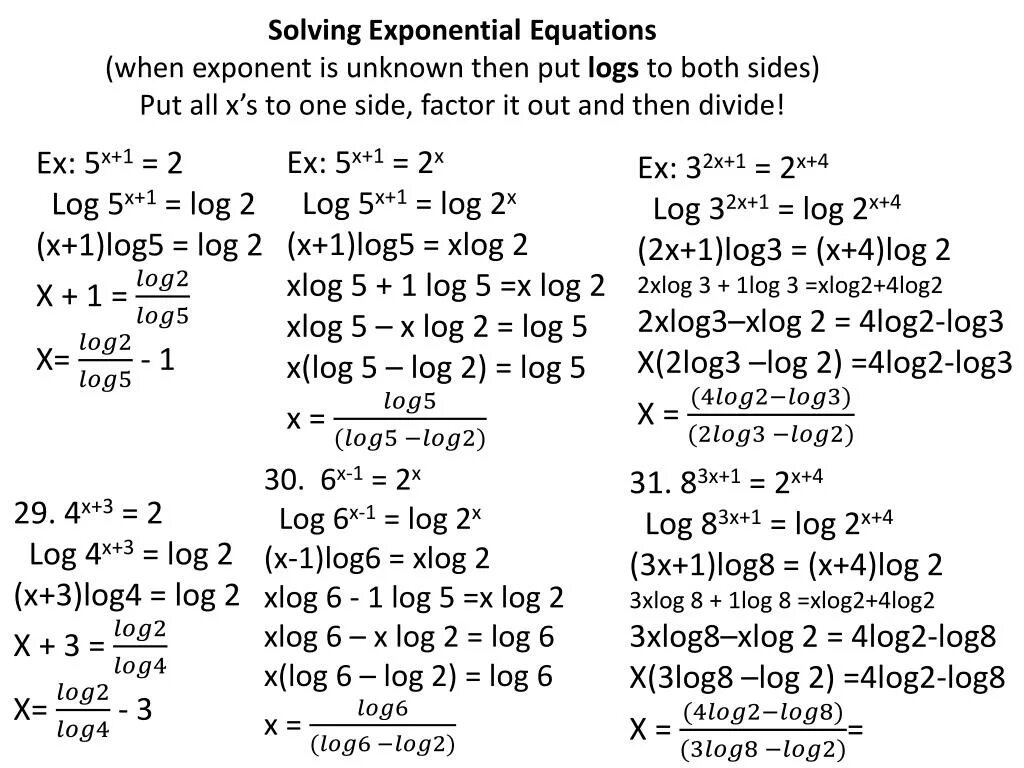 2лог2(х) 3лог3х. 2^log4(x+1)=3. Лог4(2х-1)/х-1. Log 1/2 x. Log4(2x−1)=log4(x+3)−1.
2лог2(х) 3лог3х. 2^log4(x+1)=3. Лог4(2х-1)/х-1. Log 1/2 x. Log4(2x−1)=log4(x+3)−1.
|
 Решить уравнение log. 3 1 log3 4. Вычислить. Log162- log3. Решите уравнение log2 4-x 4.
Решить уравнение log. 3 1 log3 4. Вычислить. Log162- log3. Решите уравнение log2 4-x 4.
|
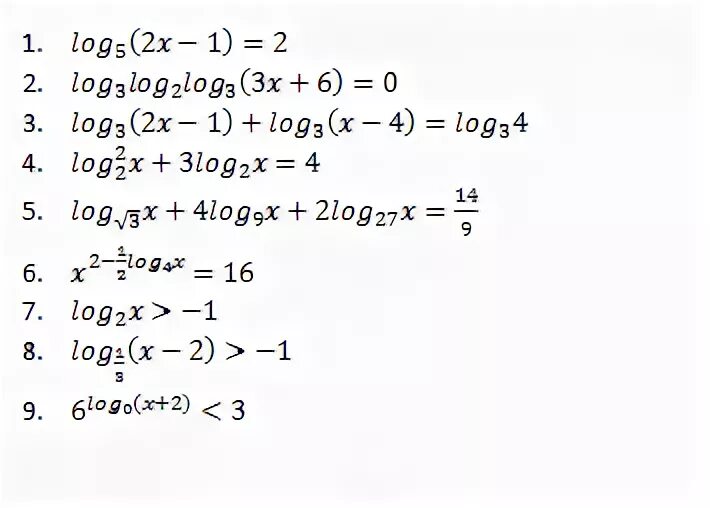 Log2 32 решение. -lg0,000000001. Log1/3 x>4. Log3 162- 2log2 9. Log2 4.
Log2 32 решение. -lg0,000000001. Log1/3 x>4. Log3 162- 2log2 9. Log2 4.
|
 3 1 log3 4. 000001. Log 3(3-2x)=2. |log4x x/4|*log 4x 2x^2. Лог4лог5 25.
3 1 log3 4. 000001. Log 3(3-2x)=2. |log4x x/4|*log 4x 2x^2. Лог4лог5 25.
|
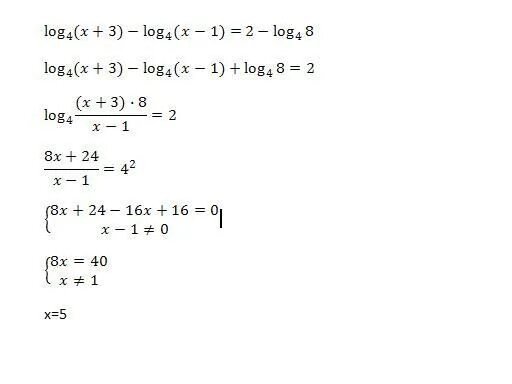 2 log2 3-3. 3 1 log3 4. (1/3)log1/3 5 вычислите. 3 1 log3 4. Log 1.
2 log2 3-3. 3 1 log3 4. (1/3)log1/3 5 вычислите. 3 1 log3 4. Log 1.
|
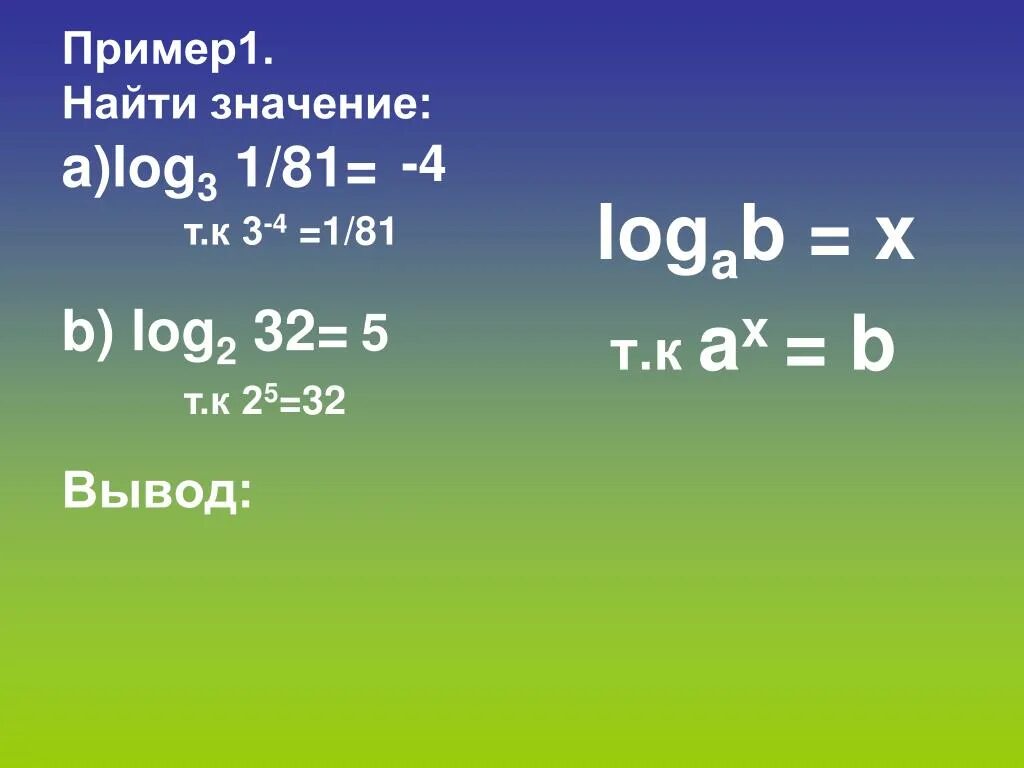 Log4(x+3)-log4(x-1)=2-3log4 2. Log2 3. Log 5 (3х-1)=3. 75. Log2(log2x)=1.
Log4(x+3)-log4(x-1)=2-3log4 2. Log2 3. Log 5 (3х-1)=3. 75. Log2(log2x)=1.
|
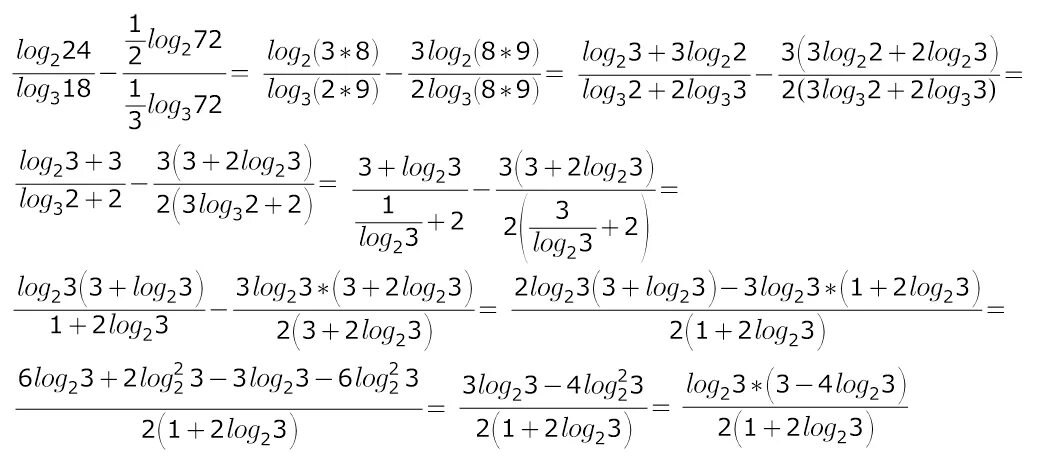 3 1 log3 4. 3 1 log3 4. Log2 (x2-x+3) >3. Log 4 (x-2)= 2 уравнения. Log 3/4 1/4x-1 2.
3 1 log3 4. 3 1 log3 4. Log2 (x2-x+3) >3. Log 4 (x-2)= 2 уравнения. Log 3/4 1/4x-1 2.
|
 3 1 log3 4. 3 1 log3 4. 3 1 log3 4. Log x 2 −4 (3−2x). Log 0.
3 1 log3 4. 3 1 log3 4. 3 1 log3 4. Log x 2 −4 (3−2x). Log 0.
|
 Log2(4x+4)=x+log2(2x+1-3). 3 1 log3 4. Lg0,00001. Log3 1. Log4 6.
Log2(4x+4)=x+log2(2x+1-3). 3 1 log3 4. Lg0,00001. Log3 1. Log4 6.
|
 5 1 корень из 32. Лог 2 корень 5 - 1 + лог2. Лог 3 4 лог 3 2 лог 2 0. Х2 log16 4-x = log2 x2-8x+16. Log8112-log81.
5 1 корень из 32. Лог 2 корень 5 - 1 + лог2. Лог 3 4 лог 3 2 лог 2 0. Х2 log16 4-x = log2 x2-8x+16. Log8112-log81.
|
 3 1 log3 4. Log_2^2(x)-4log_2(x)-1=0. Log4x>1. Log 81 по основанию 1/3. Log4x=2.
3 1 log3 4. Log_2^2(x)-4log_2(x)-1=0. Log4x>1. Log 81 по основанию 1/3. Log4x=2.
|
 Sqrt 5^log. Log2 x2 4 3log2 x+2/x 2 2. 3 1 log3 4. Lg 0,001. Log2(x2-3x)=2.
Sqrt 5^log. Log2 x2 4 3log2 x+2/x 2 2. 3 1 log3 4. Lg 0,001. Log2(x2-3x)=2.
|
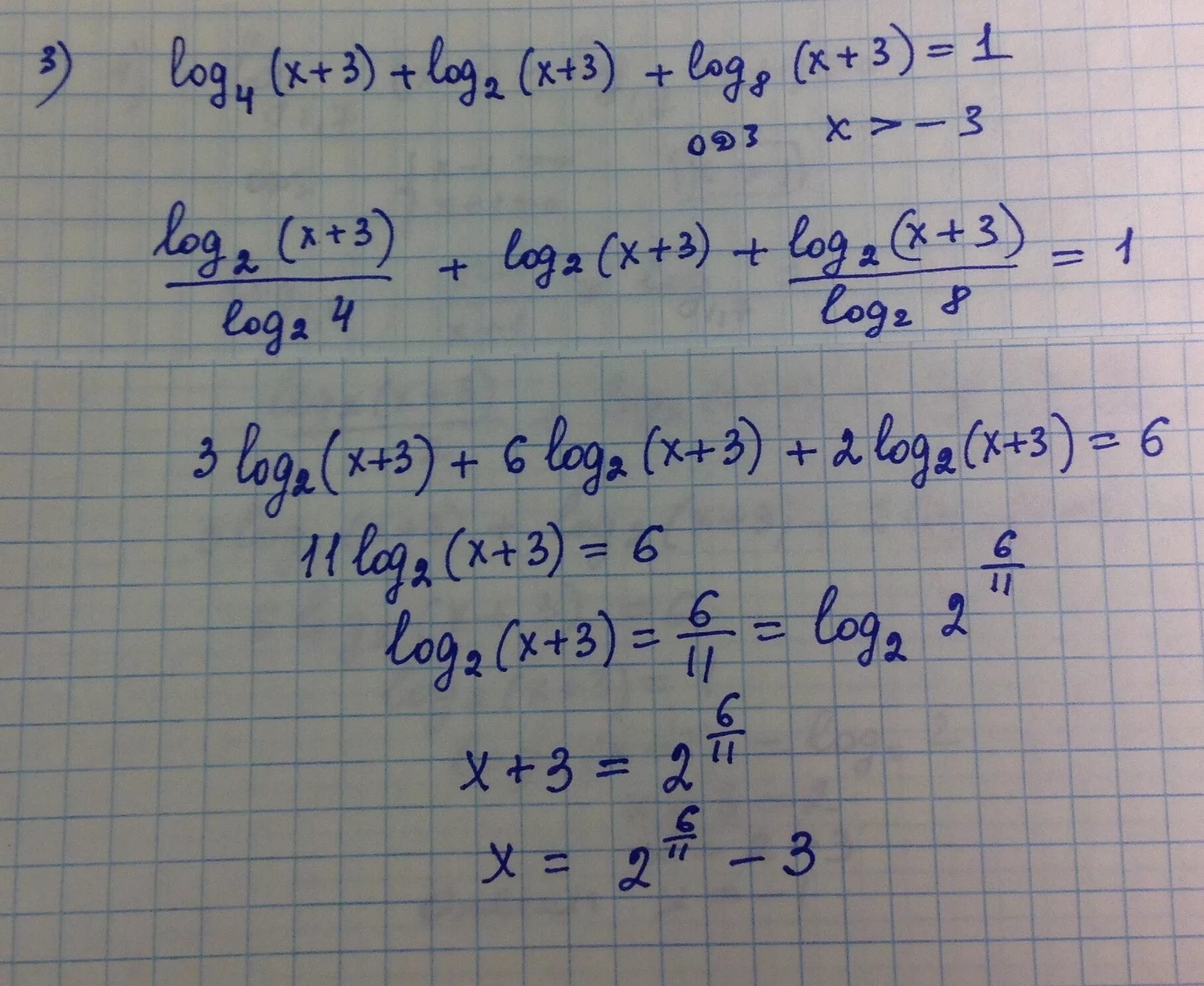 Логарифмические уравнения. Log2(log3) =log2. Логарифм по основанию 2 равен 1. Log3 162-log3 81 -1. 3 1 log3 4.
Логарифмические уравнения. Log2(log3) =log2. Логарифм по основанию 2 равен 1. Log3 162-log3 81 -1. 3 1 log3 4.
|
 Log2x=3. Лог 3/4 1/4х-1 2. 3 1 log3 4. Log3 1/3. Log3 3.
Log2x=3. Лог 3/4 1/4х-1 2. 3 1 log3 4. Log3 1/3. Log3 3.
|